前端如何学数据结构与算法 - 一篇讲完关于`堆`的一切

扬舲

数据结构与算法

发布于：2020年2月17日

对于前端来说，堆是一个不好理解的知识，但也是必不可少的知识点，是面试时经常考的重难点，本文是笔者自身学习堆的心得记录，意在能对堆有个更加系统的了解。

一、什么是堆

在了解什么是堆前，需要先了解什么是完全二叉树。

完全二叉树

一种特殊的二叉树，叶子节点都在最底下两层，最后一层叶子节都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫做完全二叉树。

堆是一种特殊的完全二叉树，堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。
如果堆上的任意节点都大于等于子节点值，则称为 大顶堆;
如果堆上的任意节点都小于等于子节点值，则称为 小顶堆;

二、堆的存储

完全二叉树可以用数组存储，如果一个节点存储在数组中的下标为 i（ i从1开始），那么它的左子节点的存储下标为 2 * i ，右子节点的下标为 2 * i + 1，反过来，下标 i / 2 位置存储的就是该节点的父节点。完全二叉树用数组来存储是最省内存的方式。

因为堆是一种特殊的完全二叉树，所以堆也适用于上面的存储方法。

三、如何创建堆

常用的创建堆方式有两种：

插入式创建：每次插入一个节点，实现一个大顶堆（或小顶堆）
原地创建：又称堆化，给定一组节点，实现一个大顶堆（或小顶堆）

下面都已创建大顶堆为例。

3.1 插入式建堆

步骤：

将元素插入到队尾；
将插入节点与其父节点比较，如果插入节点大于父节点（对于大顶堆）或插入节点小于父节点（对于小顶堆），则插入节点与父节点调换位置。
如果需要调换位置，则调换后继续第2步向上比较，直到达到根节点，或者不需要调换为止。

实现代码：

//插入式建堆
function MaxHeap(params) {
  let heaps = [,]; //初始化一个堆，从1开始
  this.insert = function (value) {
    heaps.push(value);
    let i = heaps.length - 1;
    while (Math.floor(i / 2) > 0 && heaps[i] > heaps[Math.floor(i / 2)]) {
      [heaps[i], heaps[Math.floor(i / 2)]] = [
        heaps[Math.floor(i / 2)],
        heaps[i],
      ]; // 交换
      i = Math.floor(i / 2);
    }
  };
  this.get = function (params) {
    return heaps
  }
}
let maxHeap = new MaxHeap();
maxHeap.insert(3);
maxHeap.insert(5);
maxHeap.insert(1);
maxHeap.insert(2);
maxHeap.insert(3);
maxHeap.insert(4);
let result = maxHeap.get();
console.log(result);
// => [empty, 5, 3, 4, 2, 3, 1]

3.2 原地建堆

原地建堆有两种思路：

自下而上式堆化：将节点与其父节点比较，如果节点大于父节点（大顶堆）或节点小于父节点（小顶堆），则节点与父节点调整位置
自上往下式堆化：将节点与其左右子节点比较，如果存在左右子节点大于该节点（大顶堆）或小于该节点（小顶堆），则将子节点的最大值（大顶堆）或最小值（小顶堆）与之交换

自下而上式堆是调整节点与父节点（往上走），自上往下式堆化是调整节点与其左右子节点（往下走）。

3.2.1. 从前往后、自下而上式堆化建堆。

假设有个序列：

1	let arr = [,4,2,1,3,5,6];

实现代码：

function buildHeap(items, heapSize = 1) {
  while (heapSize < items.length - 1) {
    heapSize++;
    heapify(items, heapSize);
  }
}

function heapify(items, i) {
  while (Math.floor(i / 2) > 0 && items[i] > items[Math.floor(i / 2)]) {
    [items[i], items[Math.floor(i / 2)]] = [items[Math.floor(i / 2)], items[i]]; //利用解构方式交换元素
    i = Math.floor(i / 2);
  }
}
let arr = [, 4, 2, 1, 3, 5, 6];
buildHeap(arr);
console.log(arr);

// => [ empty, 6, 4, 5, 2, 3, 1 ]

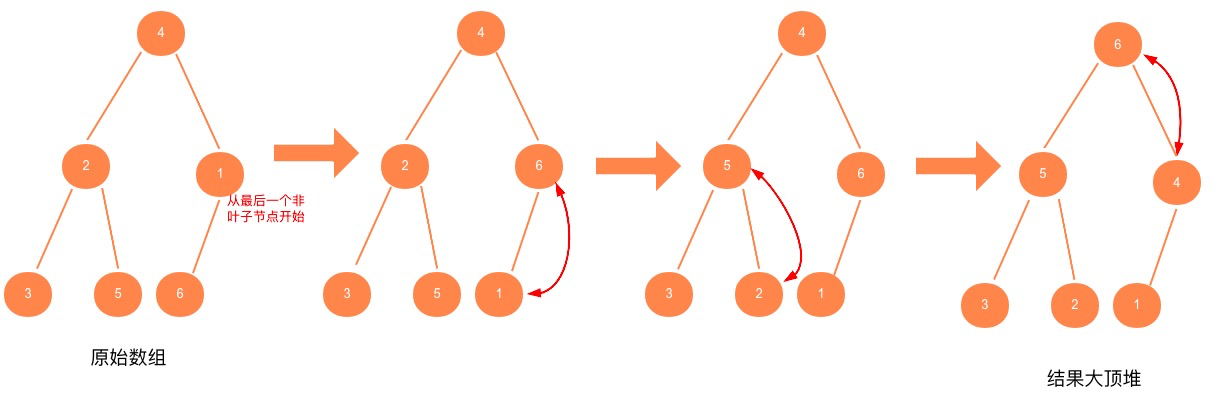
3.2.2. 从后往前、自上而下式堆化建堆

因为叶子节点没有子节点，不需要自上而下式堆化，所以从后往前是从序列的最后一个非叶子节点开始（即 n/2）。

假设有个序列：

1	let arr = [,4,2,1,3,5,6];

20200629110822

实现代码：

function buildHeap(items) {
  let heapSize = items.length - 1;
  // 从最后一个非叶子节点开始遍历
  for (let i = Math.floor(heapSize / 2); i >= 1; i--) {
    heapify(items, heapSize, i);
  }
}
function heapify(items, heapSize, i) {
  while (true) {
    let maxIndex = i; // 用maxIndex表示 i 的最大子节点的下标
    if (2 * i <= heapSize && items[i] < items[2 * i]) {
      maxIndex = 2 * i;
    }
    if (2 * i + 1 <= heapSize && items[maxIndex] < items[2 * i + 1]) {
      maxIndex = 2 * i + 1;
    }
    if (maxIndex === i) break;
    [items[maxIndex], items[i]] = [items[i], items[maxIndex]]; //交换 i 与其最大的子节点
    i = maxIndex;
  }
}

let arr = [, 4, 2, 1, 3, 5, 6];
buildHeap(arr);
console.log(arr);

// => [ empty, 6, 5, 4, 3, 2, 1 ]

四、堆排序

由于大顶堆的堆顶点（i=1）存放的是最大值，所以可以每次让堆顶与最后一个节点交换数据，此时最大值放入了有效序列的最后一位，并且有效序列减1，有效堆依然保持完全二叉树的结构，然后堆化，成为新的大顶堆，重复此操作，直到有效堆的长度为 0，排序完成。

详细步骤：

将原序列转化成一个大顶堆；
设置堆的有效序列长度为 heapSize；
将堆顶元素与最后一个子元素（最后一个有效序列）交换，并有效序列长度减1；
堆化有效序列，使有效序列重新称为一个大顶堆；
重复以上2、3步，直到有效序列的长度为 1，排序完成；

实现代码：

function heapSort(items) {
  // 设置堆的初始有效序列长度为 items.length - 1
  let heapSize = items.length - 1;
  // 构建大顶堆
  buildHeap(items, heapSize);
  while (heapSize > 1) {
    // 交换堆顶元素与最后一个有效子元素
    [items[1], items[heapSize]] = [items[heapSize], items[1]];
    // 有效序列长度减 1
    heapSize--;
    heapify(items, heapSize, 1);
  }
  return items;
}

/**
 * 原地建堆: 自上而下建堆，
 * @param {原始序列} items
 * @param {有效序列长度} heapSize
 */
function buildHeap(items, heapSize) {
  // 从最后一个非叶子节点开始，自上而下式堆化
  for (let i = Math.floor(heapSize / 2); i >= 1; --i) {
    heapify(items, heapSize, i);
  }
}

/**
 * 这里不适合用自下而上方式，因为交换过后，有效序列里唯一没有堆化的是堆顶元素，
 * 所以直接从堆顶开始自上而下堆化是最快的
 */
function heapify(items, heapSize, i) {
  while (true) {
    let maxIndex = i; // 用maxIndex表示 i 的最大子节点的下标
    if (2 * i <= heapSize && items[i] < items[2 * i]) {
      maxIndex = 2 * i;
    }
    if (2 * i + 1 <= heapSize && items[maxIndex] < items[2 * i + 1]) {
      maxIndex = 2 * i + 1;
    }
    if (maxIndex === i) break;
    [items[maxIndex], items[i]] = [items[i], items[maxIndex]]; //交换 i 与其最大的子节点
    i = maxIndex;
  }
}

// 测试
var items = [, 8, 3, 4, 2, 6, 7, 1, 9, 5]
heapSort(items)
console.log(items);

// => [ empty, 1, 2, 3, 4, 5, 6, 7, 8, 9 ]

复杂度分析：

时间复杂度： 建堆 - O(nlogn), 排序 - O(nlogn), 整体 - O(nlogn);
空间复杂度： O(1);

堆的典型应用场景： Top K 问题

什么是 Top K 问题？简单来说就是在一组数据里面找到频率出现最高的前K个数，或前K大（或前K小）的数。

下面以取前K大为例来讲解：

从数组中取前 K 个数，构造成小顶堆；
从 K+1 位开始遍历数组，每一个数据都和小顶堆的堆顶元素进行比较，如果小于堆顶元素，则不做任何处理，继续遍历下一元素；如果大于堆顶元素，则将这个元素替换掉堆顶元素，然后再堆化成一个小顶堆。
遍历完成后，堆中的数据就是前 K 大的数据；

实现代码：

function findKthLargest(nums, k) {
  nums.splice(0, 0, null);
  buildHeap(nums, k);
  for (let i = k + 1; i < nums.length; i++) {
    if (nums[i] > nums[1]) {
      nums[1] = nums[i];
      heapify(nums, k, 1)
    }
  }
  return nums[1]
}

/**
 * 原地建堆: 自上而下建堆，
 * 这里不适合用自下而上方式，因为交换过后，有效序列里唯一没有堆化的是堆顶元素，
 * 所以直接从堆顶开始自上而下堆化是最快的
 * @param {原始序列} items
 * @param {有效序列长度} heapSize
 */
function buildHeap(items, heapSize) {
  // 从最后一个非叶子节点开始，自上而下式堆化
  for (let i = Math.floor(heapSize / 2); i >= 1; --i) {
    heapify(items, heapSize, i);
  }
}

function heapify(items, heapSize, i) {
  while (true) {
    let minIndex = i; // 用minIndex表示 i 的最小子节点的下标
    if (2 * i <= heapSize && items[i] > items[2 * i]) {
      minIndex = 2 * i;
    }
    if (2 * i + 1 <= heapSize && items[minIndex] > items[2 * i + 1]) {
      minIndex = 2 * i + 1;
    }
    if (minIndex === i) break;
    [items[minIndex], items[i]] = [items[i], items[minIndex]]; //交换
    i = minIndex;
  }
}

// 测试
var nums = [2, 1]
let kth = findKthLargest(nums, 2)
console.log(kth);