扬舲blog

leetCode题解记录

数组类

常用方法总结：

  • 结合Object(Map/set)等数据结构来解题；
  • 滑动窗口方法（最小（大）子集等问题适用）
  • Trie 树

两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

1
2
3
4
给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

方法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var twoSum = function(nums, target) {
    let result = [];
    for(let i = 0, length = nums.length; i < length; i++){
        const left = target - nums[i];
        const leftIndex = nums.lastIndexOf(left);
        if(leftIndex > i){
            result = [i ,leftIndex];
            break;
        }
    }
    return result;
};

复杂度分析：

  • 时间复杂度：O(n2)
  • 空间复杂度：o(1)

方法二：

1
2
3
4
5
6
7
8
9
10
11
var twoSum = function(nums, target) {
    let map = new Map()
    for(let i = 0; i< nums.length; i++) {
        let k = target-nums[i]
        if(map.has(k)) {
            return [map.get(k), i]
        }
        map.set(nums[i], i)
    }
    return [];
};

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：o(n)

15. 三数之和

解题思路：

  1. 首先对数组从大到小进行排序；
  2. 遍历数组，设置左右俩指针初始位置在数组左右边界（first = i + 1,last = length -1）;
  3. 如果i, first, last 三个数值大于0，则last左移，如果小于0，则first右移；
  4. 使得最终三数之和等于0，则成功找出一组。重复步骤2。

实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

var threeSum = function (nums) {
  let res = [];
  let length = nums.length;
  nums.sort((a, b) => a - b); // 先排个队，最左边是最弱（小）的，最右边是最强(大)的
  if (nums[0] > 0 || nums[length - 1] < 0) {
    return res;
  }
  for (let i = 0; i < length - 2; i) {
    if (nums[i] > 0) break;
    let first = i + 1, last = length - 1, sum;
    while (first < last) {
      sum = nums[i] + nums[first] + nums[last];
      if (sum === 0) {
        res.push([nums[i], nums[first], nums[last]]);
        while (first < last && nums[first] === nums[++first]) { }
      } else if (sum < 0) {
        while (first < last && nums[first] === nums[++first]) { }
      } else {
        while (first < last && nums[last] === nums[--last]) { }
      }
    }
    while (nums[i] === nums[++i]) { }
  }
  return res;
};

复杂度分析

  • 时间复杂度： O(n2)

16. 最接近的三数之和

解题思路

思路同上一题类似，不同点在于此题是求最接近给定值的解。

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
var threeSumClosest = function (nums, target) {
  nums.sort((a, b) => a - b);
  let length = nums.length;
  let result = nums[0] + nums[1] + nums[length - 1];
  for (let i = 0; i < length - 2; i++) {
    let first = i + 1;
    let last = length - 1;
    let sum;
    while (first < last) {
      sum = nums[i] + nums[first] + nums[last];
      sum > target ? last-- : first++;
      if (Math.abs(target - result) > Math.abs(target - sum)) {
        result = sum;
      }
    }
  }
  return result;
};

复杂度分析

  • 时间复杂度： O(n2)

最大子序和

算法：

在整个数组或在固定大小的滑动窗口中找到总和或最大值或最小值的问题可以通过动态规划（DP）在线性时间内解决。
有两种标准 DP 方法适用于数组：

  1. 常数空间，沿数组移动并在原数组修改。
  2. 线性空间，首先沿 left->right 方向移动，然后再沿 right->left 方向移动。 合并结果。

我们在这里使用第一种方法，因为可以修改数组跟踪当前位置的最大和。
下一步是在知道当前位置的最大和后更新全局最大和。

Jk1psf.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * @param {number[]} nums
 * @return {number}
 */var maxSubArray = function (nums) {
  if (nums.length === 1) {
    return nums[0];
  }
  let maxSum = nums[0];
  for (let i = 1, length = nums.length; i < length; i++) {
    if (nums[i - 1] > 0) nums[i] += nums[i - 1]; // index位上的值变为到这位为止的最大值
    maxSum = Math.max(nums[i], maxSum); // 取当前位与历史位的最大值
  }
  return maxSum;
};

复杂度分析:

  • 时间复杂度：O(N)。只遍历了一次数组。

  • 空间复杂度：O(1)，使用了常数的空间。

239. 滑动窗口最大值

解题思路

  • 使用 队列 方式维护一个滑动窗口内的数值索引，并确保队列队首值是当前滑动窗口的最大值索引
  • 对应索引i来说，在i前面并且比i的值小的数值是没有价值的，可以剔除掉

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
var maxSlidingWindow = function (nums, k) {
  //queue保存 SlidingWindow 数据，其中首位是最大值的索引
  const queue = [], result = [];
  for (let i = 0; i < nums.length; i++) {
    //剔除SlidingWindow外的数据
    if (i - queue[0] >= k) {
      queue.shift();
    }
    // 剔除queue元素，确保queue首位保存的是最大值的索引
    while (nums[i] > nums[queue[queue.length - 1]]) {
      queue.pop()
    }
    queue.push(i)
    //从k-1开始输出结果
    if (i >= k - 1) {
      result.push(nums[queue[0]])
    }
  }
  return result;
}

合并两个有序数组

给你两个有序整数数组 nums1 和 nums2，请你将 nums2 合并到 nums1 中，使 nums1 成为一个有序数组。

说明:

初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。
你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。
示例:

1
2
3
4
5
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6],       n = 3

输出: [1,2,2,3,5,6]

思路分析：
nums1 、 nums2 有序，若把 nums2 全部合并到 nums1 ，则合并后的 nums1 长度为 m+n
我们可以从下标 m+n-1 的位置填充 nums1，循环比较 nums1[len1] 与 nums2[len2] 的大小，将最大值写入 nums1[len]。
边界条件：

  • 若 len1 < 0， len2 >= 0 ，此时 nums1 已重写入， nums2 还未合并完，只需将 nums2 的剩余元素写入 nums1 即可，写入后，合并完成；
  • 若 len2 < 0，此时 nums2 已全部合并到 nums1 ，合并完成。

实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * @param {number[]} nums1
 * @param {number} m
 * @param {number[]} nums2
 * @param {number} n
 * @return {void} Do not return anything, modify nums1 in-place instead.
 */
var merge = function (nums1, m, nums2, n) {
  let len1 = m - 1,
    len2 = n - 1,
    len = m + n - 1;
  //若len2 < 0,说明 nums2 已全部合并到 nums1 ，合并完成
  while (len2 >= 0) {
    if (len1 < 0) {
      // 此时 nums1 已重写入， nums2 还未合并完，仅仅需要将 nums2 的剩余元素写入 nums1 即可
      nums1[len--] = nums2[len2--];
      continue;
    }
    nums1[len--] = nums1[len1] >= nums2[len2] ? nums1[len1--] : nums2[len2--]
  }
};

复杂度分析：

  • 时间复杂度为 O(m+n)
  • 空间复杂度为 O(1）

14. 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 “”。
示例 1:

1
2
输入: ["flower","flow","flight"]
输出: "fl"

示例 2:

1
2
3
输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

解题思路：

本题的解题方法很多，比如：

  1. 直接逐个比较;
  2. 寻找最大字符串与最小字符串，将问题化解为比较这两个字符串的大小（ace > acd > abc => 这三个字符串的最长公共前缀一定是ace与abc两者的最长公共前缀）
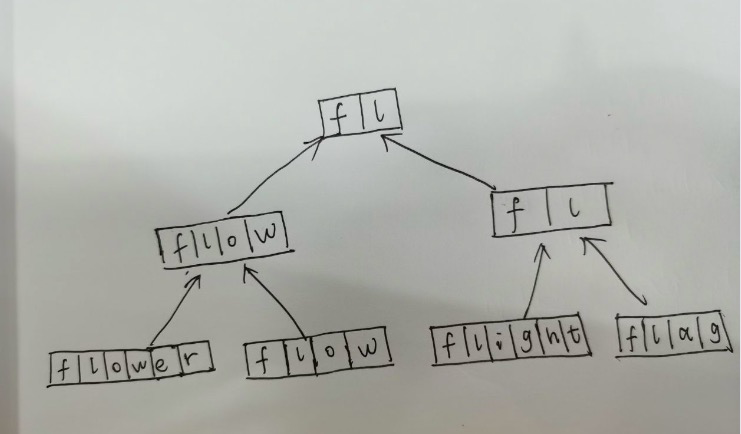
  3. 分治/归并策略： 将问题分解为每两个字符串的最长公共前缀，再归并为一，求得最后值。如下图：

  1. 利用Trie 树（字典树）
    Trie 树，也称为字典树或前缀树，顾名思义，它是用来处理字符串匹配问题的数据结构，以及用来解决集合中查找固定前缀字符串的数据结构。

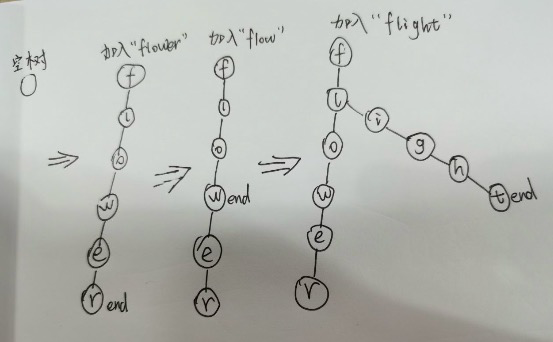
下面以Trie树方式为例来实现，思路如下：
构建一个 Trie 树，字符串数组的最长公共序列就为从根节点开始遍历树，直到：

  • 遍历节点存在超过一个子节点的节点

  • 或遍历节点为一个字符串的结束字符

为止，走过的字符为字符串数组的最长公共前缀。

如图，以[“flower”,”flow”,”flight”]为例，最终结果为"fl"
20200622162347

实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
var longestCommonPrefix = function (strs) {
  if (strs === null || strs.length === 0) return "";
  // 初始化 Trie 树
  let trie = new Trie()
  // 构建 Trie 树
  for (let i = 0; i < strs.length; i++) {
    if (!trie.insert(strs[i])) return ""
  }
  // 返回最长公共前缀
  return trie.searchLongestPrefix()
};

var TrieNode = function () {
  // next 放入当前节点的子节点
  this.next = {};
  // 当前是否是结束节点
  this.isEnd = false;
};

// Trie 树
var Trie = function () {
  this.root = new TrieNode()
};

Trie.prototype.insert = function (word) {
  if (!word) return false
  let node = this.root
  for (let i = 0; i < word.length; i++) {
    if (!node.next[word[i]]) {
      node.next[word[i]] = new TrieNode()
    }
    node = node.next[word[i]]
  }
  node.isEnd = true
  return true
};
Trie.prototype.searchLongestPrefix = function () {
  let node = this.root
  let prevs = ''
  while (node.next) {
    let keys = Object.keys(node.next)
    if (keys.length !== 1) break; //超过一个子节点的节点
    if (node.next[keys[0]].isEnd) { //节点为一个字符串的结束字符
      prevs += keys[0]
      break
    }
    prevs += keys[0]
    node = node.next[keys[0]]
  }
  return prevs
}

const res = longestCommonPrefix(["flower", "flow", "flight"])
console.log(res);

链表类

常用方法总结：

  • 快慢指针
  • 标记位法

合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例：

1
2
输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

思路
从链表头开始比较，l1 与 l2 是有序递增的，所以比较 l1.val 与 l2.val 的较小值就是合并后链表的最小值，次小值就是小节点的 next.val 与大节点的 val 比较的较小值，依次递归，直到递归到 l1 l2 均为 null

确定边界条件： 当递归到任意链表为 null ，直接将 next 指向另外的链表即可，不需要继续递归了

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function mergeTwoLists(l1, l2) {
    if(l1 === null) {
        return l2
    }
    if(l2 === null) {
        return l1
    }
    if(l1.val <= l2.val) {
        l1.next = mergeTwoLists(l1.next, l2)
        return l1
    } else {
        l2.next = mergeTwoLists(l2.next, l1)
        return l2
    }
}

141. 环形链表

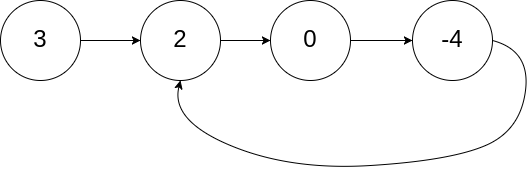
给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：

1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

20200622140709

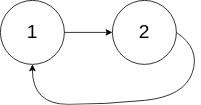
示例 2：

1
2
3
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

1
2
3
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

方法一：标志法
给每个已遍历过的节点加标志位，遍历链表，当出现下一个节点已被标志时，则证明单链表有环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
    while(head){
        if(head.flag){
            return true;
        }
        head.flag = 1;
        head = head.next;
    }
    return false
};

方法二： 快慢指针法
设置快慢两个指针，遍历单链表，快指针一次走两步，慢指针一次走一步，如果单链表中存在环，则快慢指针终会指向同一个节点，否则直到快指针指向 null 时，快慢指针都不可能相遇。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
var hasCycle = function(head) {
    if(!head || !head.next) {
        return false
    }
    let fast = head.next.next, slow = head.next;
    while(fast && fast.next){ // fast.next为null说明fast是链表终点，无环
        if(fast === slow ){
            return true
        }
        fast = fast.next.next;
        slow = slow.next;
    }
    return false;
};

方法三： 利用 JSON.stringify() 不能序列化含有循环引用的结构

1
2
3
4
5
6
7
8
9
var hasCycle = function(head) {
    try{
        JSON.stringify(head);
        return false;
    }
    catch(err){
        return true;
    }
};

142. 环形链表 II

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

解题思路：

本题与上一题类似，增加的难度在于需要返回入环点。所以无法基于JSON.stringify()来实现了。
方法一： 标志法
此方法实现代码与上一题基本一样，只是返回值有所区别。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function (head) {
    while(head){
        if(head.flag){
            return head;
        }
        head.flag = 1;
        head = head.next;
    }
    return null;
};

方法二： 快慢指针法

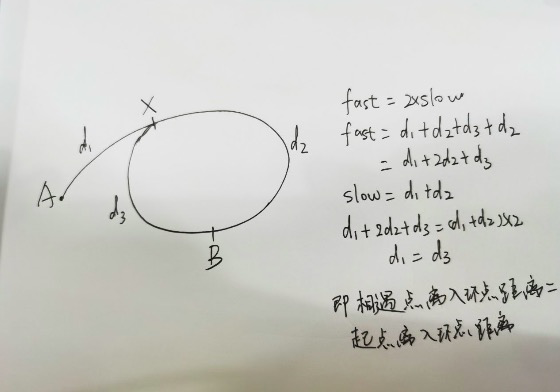
上一题中快慢指针相遇点（即fast === slow）肯定是环内某一点（注意不一定是入环点，所以本题不能直接返回这个节点）。

所以接下去主要工作是如何判断入环点？

基于上一题，我们设置fast指针速度是2，slow指针速度是1, fast速度是slow速度的2倍，所以最终相遇（fast === slow）时，fast走的距离也是slow走的距离的2倍。
具体分析如下：

1
2
3
4
5
6
A - 起点
B - 第一次相遇点
X - 入环点
d1 - A-X距离
d2 - X-B距离
d3 - B-X距离

20200622145207

最后得出d1 = d3。那么就可以在上题基础上进行寻找入环点：

当fast和slow在B点相遇后，将fast重回A点。将两个指针均以速度1向前走，最终会在X点相遇（距离一样，速度一样，所以到X点的时间也一样），相遇时返回节点即可。

实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
var detectCycle = function (head) {
    if(!head || !head.next) {
        return null
    }
    let fast = head.next.next, slow = head.next;
    while(fast && fast.next){//fast.next为null说明fast是链表终点，无环
        if(fast === slow ){
            fast = head;
            while(fast !== slow){
                fast = fast.next;
                slow = slow.next;
            }
            return slow;
        }
        fast = fast.next.next;
        slow = slow.next;
    }
    return null;
};

反转链表

解题思路：

定义一个反转链表prev, 循环head指针，将当前head指向prev，实现反转效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function(head) {
    let prev = null;
    while(head){
        //临时存放下一个指针
        let next = head.next;
        //将当前节点指向prev，实现反转效果
        head.next = prev;
        // 变更prev、head
        prev = head;
        head = next;
    }
    return prev;
};

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

19. 删除链表的倒数第N个节点

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。
示例：

1
2
3
给定一个链表: 1->2->3->4->5, 和 n = 2.

当删除了倒数第二个节点后，链表变为 1->2->3->5.

解题思路：
需要删除链表中的倒数第 n 个节点，我们需要知道的就是倒数第 n+1 个节点，然后删除删除倒数第 n+1 节点的后继节点即可.

使用快慢指针思想来解决此问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var removeNthFromEnd = function(head, n) {
    let fast = head, slow = head
    // 快先走 n - 1 步
    while(--n) {
        fast = fast.next
    }
    if(!fast.next) return head.next;//说明列表长度为n,删除头结点
    fast = fast.next
    // fast、slow 一起前进
    while(fast && fast.next) {
        fast = fast.next
        slow = slow.next
    }
    slow.next = slow.next.next
    return head
};

876. 链表的中间结点

解题思路：
使用快慢指针方法： 快指针速度2，慢指针速度1，当快指针到达终点时，慢指针刚好在中间节点。

1
2
3
4
5
6
7
8
var middleNode = function(head) {
    let fast = head, slow = head;
    while(fast && fast.next){
        fast = fast.next.next;
        slow = slow.next;
    }
    return slow;
};

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

动态规划类

309. 最佳买卖股票时机含冷冻期

分析：

第i天主要有三种情况，当天收益取三者最大值：

  1. 当天持有此股票，那么股票可能是：
    a. 前一天就持有的, 取值(dp[i - 1][0])，
    b. 或者当天刚买的,取值(dp[i - 1][2] - prices[i]))，
    这种情况的最大收益为： Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i]);

  2. 当天卖出股票，则收益为前一天的持有收益 + 当天的股票价格收益， 即： dp[i - 1][0] + prices[i];

  3. 当天未持有，并且当天未卖出过，则有两种情况：
    a. 前一天卖出过，dp[i-1][1]
    b. 前一天未卖出， dp[i-1][2]。
    这种情况的最大收益为： Math.max(dp[i - 1][1], dp[i - 1][2]);

    第一天的初始值：dp[0] = [-prices[0], 0, 0];

    代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*
 * 最终的收益是当天的三种情况取最大
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function (prices) {
  const len = prices.length;
  if (len < 2) return 0
  const dp = [];
  dp.push([-prices[0], 0, 0]);
  let t0, t1, t2;
  for (let i = 1; i < len; i++) {
    t0 = Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i]); // 当天持有此股票
    t1 = dp[i - 1][0] + prices[i]; // 当天未持有，并且当天卖出
    t2 = Math.max(dp[i - 1][1], dp[i - 1][2]); //当天未持有，并且不是当天卖出
    dp.push([t0, t1, t2]);
  }

  return Math.max(...dp.pop())
};

面试题 17.13. 恢复空格

分析：
遍历 sentence，如果i-1结尾的子字符串 等于 dictionary的某个word, 说明dp[i] 可以等于 dp[i - word.length]；

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @param {Array} dictionary
 * @param {String} sentence
 * @return {number}
 */

const respace = (dictionary, sentence) => {
  const len = sentence.length;
  if (len === 0) return 0;
  const dp = new Array(len + 1);
  dp[0] = 0;
  for (let i = 1; i <= len; i++) { //i代表 Length(sentence)
    dp[i] = dp[i - 1] + 1;
    for (const word of dictionary) {
      if (word === sentence.substring(i - word.length, i)) {
        dp[i] = Math.min(dp[i], dp[i - word.length])
      }
    }
  }

  return dp[len]
};

96. 不同的二叉搜索树

  • 思路:
    标签：动态规划
    假设n个节点存在二叉排序树的个数是dp(n)，令f(i)为以i为根的二叉搜索树的个数，则
    dp(n) = f(1) + f(2) + f(3) + f(4) + … + f(n)

当i为根节点时，其左子树节点个数为i-1个，右子树节点为n-i，则
f(i) = dp(i-1)*dp(n-i)

综合两个公式可以得到 卡特兰数 公式
dp(n) = dp(0)dp(n-1)+dp(1)(n-2)+…+dp(n-1)*dp(0)

  • 代码实现：
1
2
3
4
5
6
7
8
9
10
11
var numTrees = function (n) {
  const dp = new Array(n + 1).fill(0);
  dp[0] = 1;
  dp[1] = 1;
  for (let i = 2; i <= n; i++) {
    for (let j = 1; j <= i; j++) { //以j为顶点的个数计算
      dp[i] += dp[j - 1] * dp[i - j];
    }
  }
  return dp[n];
}

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：http://blog.kobingo.xyz/algorithms-leetcode/

评论